what units would you use to measure a virus
Contents
- 1 Learning Outcomes
- 2 Prelab
- 3 Metric base units and their prefixes
- 3.1 Metric Units for Biology:
- 3.2 Table 1.four Metric Prefixes
- 3.3 Metric staircase
- 3.4 Factoring Out
- 3.5 Practise conversions (THIS CAN Exist A H5p EXERCISE)
- iv Accuracy and PRECISION
-
- four.0.ane Lab Activeness:
-
- 5 Length
Learning Outcomes
-
- To explicate the demand of a universal organization of measurements in science.
- To recall the metric base units and their prefixes.
- To be able to make metric conversions.
- To deport out calculations using numbers in scientific note.
- To appreciate the difference between Precision and Accuracy
- To exist able to tape and calculate data with proper significant figures.
- To learn about the key steps in the scientific method
- To identify and listing the variables in an experiment
- To place the parts of graphs and describe graphs based on a given data set.
Prelab
How alpine are you? __________
How much do yous weight? (nosotros will not double check so feel free to exist creative) _________
How much liquid is in a can of soda? ____________
How much rice is in the bag yous but got at the shop? ___________
What units did you use to answer these questions? ________________
Expect at the can of soda or rice bag (or any other item you lot cull for the exercise).
What units do you observe on the container?
What is the departure?
Accept you heard of Imperial Units and Metric Units? Which i on the can of soda exercise you call back is an Imperial Unit and which is a Metric Unit of measurement?
Imperial: Metric:
Which one do you remember is the system that we will be using in our form? __________________
The standard organisation of measurement in the sciences, including biology, chemistry, and physics is the metric system , which, yous may take learned from the prelab do, information technology is non what you use in your everyday life in the United states.
In 1975, the U.S. Metric Conversion Deed was signed, declaring a national policy of "encouraging" voluntary apply of the metric organization . As you may have deduced, the switch from one system to the other did not really work and today, the United States is the simply land in the world not committed to adopting the organisation.
To give yous an thought of how the 2 organisation differ y'all can look at Tables 1.1 and 1.2. In Table ane.i you can see the conversion betwixt Royal (sometimes you lot will detect it every bit English system) and Metric system units. In table 1.2 you will find some examples of everyday measurements in the Metric system.
Tabular array 1.ane Conversion between the Imperial and the metric organisation
| Metric | Purple |
| ane cm | 0.4 inch |
| 2.54 cm | 1 inch |
| ane m | ane.ane chiliad |
| 1 km | 0.62 mile |
| 1.six km | 1 mile |
| 1 °C | 9/five + 32 °F |
| 1 Fifty | one.06 quart |
| 3.8 L | ane gallon |
| 28.35 grand | one oz |
| 453.half-dozen thou | 1 lb. |
| 1 kg | 2.2 lb. |
Do:
| Temperature |
|
| |
| Length |
|
| |
| Mass |
|
| |
| Volume |
|
Fill in the blanks in the table using the corresponding Majestic or metric system: ex. Water freezes at 32 °F
Looking at Table 1.one and ane.2 can yous list on or two interesting departure betwixt the ii systems that you can see?
The metric organization is based on decimals or powers of 10.
This 10-based organisation is like to our monetary organisation. Think
How many cents do you accept in a dime? ____ cents = one dime
How many dimes to you have in a dollar? ____ dimes = 1 dollar.
The bang-up affair near this type of system is that all conversions (going from one unit to the other) are in units of ten.
The refined version of the metric organization used in science is chosen the International System of Units (abbreviated SI ).
Metric base units and their prefixes
In biology, oftentimes we demand to depict measurements of length, volume, mass, time, temperature or amount of substance. In Table 1.3 you can find the whole list of SI Units.
Table 1.3. International System of Units
Metric Units for Biology:
-
- length: meter ( m )
-
- Liquid book: liter ( L )
-
- mass: gram ( k )
-
- time: second ( s )
-
- temperature: Celsius ( °C )
- Kelvin ( Grand ) is a unit of thermodynamic temperature and is the SI unit. The Kelvin scale is the same as the Celsius or centigrade scale but offset by 273.16, which means that 0 Yard is – 273.16°C. Biological science uses Celsius considering of the range of temperatures in which organisms alive. Ex. boilerplate torso temperature is 37°C, Room Temperature is 25°C, water boils at 100°C and freezes at 0°C
- temperature: Celsius ( °C )
- amount of substance: mole ( mol ). A mole is a number representing vi.022×x 23 of something. Ex. A pair of shoes equals 2 shoes, a mole of shoes is 6.022×1023 shoes. A dozen eggs equals 12 eggs, a mole of eggs is 6.022×x23 eggs
The metric system is based on the decimal system and follows a consequent name scheme using prefixes that indicates either a multiple of a unit or a fraction of a unit. Multiples and fractions are always expressed as powers of ten . For example, kilo gram means a thousand (x3 ) grams, mega byte means a million (10 six ) bytes; centi meter means a hundredth (10 -2 ) of a meter, milli liter means a thousandth (10 -iii ) of a liter. You can find all the prefixes in Table 1.4. The highlighted ones are the most used.
Table ane.4 Metric Prefixes
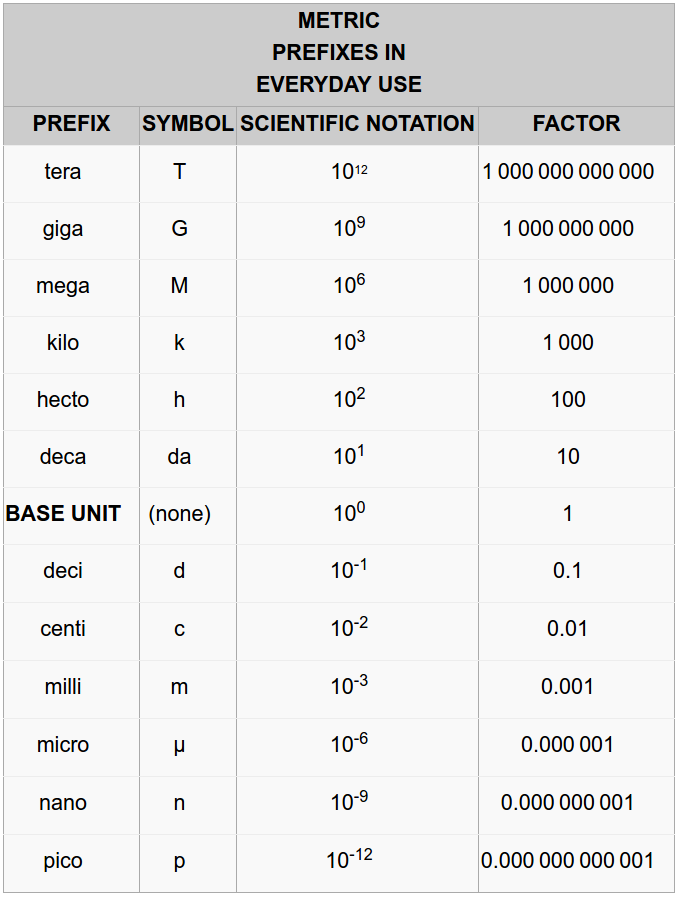
The value of the metric system is in the ease of converting from ane multiple to another since everything is in base 10 compared to the Regal system. º
Ex. 1000 mm = 1 m 1000m = 1 km compared to
12 in = 1 foot 3 feet = 1 yard 1760 yards = 1 mile
Metric conversions
Strategy for metric conversions
-
- What unit of measurement practise you lot have to catechumen to?
- 500ml = ____L → liters
- What unit of measurement practise you lot have to catechumen to?
-
- What unit are you starting from?
- 500ml → milliliters = ____L
- What unit are you starting from?
-
- Which unit of measurement is larger?
- Liters are the larger unit.
- Which unit of measurement is larger?
-
- By how much is that unit larger?
-
- Liters are 1,000X (10 iii ) greater than milliliters
- Milliliters are 1/chiliad smaller than a liter
-
- By how much is that unit larger?
- Which management are we moving? We are moving from a smaller to a larger unit (look at the tabular array), then the value volition be smaller. In this case, the value is smaller by ane,000X
In other words, the value is i/1000 or 0.001 the value.
So what is the answer? ______________
You can endeavour to visualize the conversions using a metric staircase. In the metric staircase each step represents a ten-fold change. If yous motility downwardly the staircase you multiply your value by 10 for each step or a motion the decimal one identify to the right for each step. If you movement upwardly the staircase you split up your value by x for each or move the decimal point one place to the left for each pace.
Try it for the instance higher up going from 500ml to L.
Metric staircase
Factoring Out
Using the idea of factors of ten, you lot tin assess the difference of the two units and abolish out the original unit algebraically to reach the desired concluding unit.
- 500ml=_____L
-
- 1ml =1000L or, 1L/1000ml both fraction country that at that place are 1000 milliliter in every 1 liter
- So500ml X1L/ 1000ml = 500ml X 1L/ 1000ml = 500 Ten 1L/ k = 500L/ k = .5 L
-
pay attention to the units and how we've canceled out the ml in the numerator of 500ml and in the denominator in the conversion of 1L in 1000ml.
Scientists oft work with numbers that are extremely big or extremely modest. For instance, there are 10,300,000,000,000,000,000,000 carbon atoms in a 1-carat diamond each of which has a mass of 0.000,000,000,000,000,000,000,020 grams. Information technology is impossible to multiply these numbers with most calculators considering they can't accept either number as information technology is written hither. To exercise a calculation like this, it is necessary to express these numbers in scientific notation , every bit a number between 1 and ten multiplied past 10 raised to some exponent.
Exponent Review
Some of the nuts of exponential mathematics are given below.
| Any number raised to the zero power is equal to 1. | i 0 = 1 | 10 0 = 1 | ||||
| Any number raised to the start power is equal to itself. | 1 1 = 1 | 10 1 = 10 | |||
| Any number raised to the n th power is equal to the product of that number times itself n -i times. | ||||||
| 2 2 = ii x 2 = 4 | ten 5 = x x x x 10 ten 10 x ten = 100,000 | |||||
Dividing by a number raised to an exponent is the same as multiplying by that number raised to an exponent of the opposite sign.
The post-obit rule tin can be used to convert numbers into scientific annotation: The exponent in scientific notation is equal to the number of times the decimal betoken must be moved to produce a number betwixt 1 and x.
To interpret 10,300,000,000,000,000,000,000 carbon atoms into scientific notation, we motility the decimal point to the left 22 times.
10,300,000,000,000,000,000,000 = 1.03 x ten 22
To catechumen numbers smaller than one into scientific notation, we have to move the decimal bespeak to the right. The decimal point in 0.000985, for example, must exist moved to the right four times.
0.000985 = 9.85 x ten -four
Converting 0.000000000000000000000020 grams per carbon atom into scientific notation involves moving the decimal signal to the right 23 times.
0.000000000000000000000020 = two.0 x 10 -23
The primary reason for converting numbers into scientific annotation is to make calculations with unusually big or small numbers less cumbersome. Considering zeros are no longer used to set the decimal point, all of the digits in a number in scientific annotation are significant, equally shown by the examples.
Practice conversions (THIS CAN BE A H5p Do)
Accurateness and PRECISION
In taking measurements using a particular method, it is important to know the limit of detectability , which is the smallest deviation 1 tin detect. The significant figures are the number of digits one tin can read directly using the measuring device. One can sometimes estimate an additional meaning figure. Within the limit of detectability, accuracy is how close your measurement is to the truthful value. Your accuracy may be express by the available engineering. You may have to exist satisfied with an approximation , which is a value that is not exact. Precision is the degree of agreement between several measurements. Your information may exist precise but not necessarily accurate because of flaws in the procedure. In science, results obtained by one person need to exist reproduced past others before they tin be accepted. Artifacts may be introduced by external factors, leading to incorrect conclusions.
Accuracy refers to how closely a measured value agrees with the correct or target value.
Precision refers to how closely private measurements agree with each other and reflects a repeatability in those measurements.

This illustrates accuracy. Measurements are on target.

This illustrates precision. Measurements are very close to each other and repeatable.

This illustrates Accuracy AND Precision. Each measurement is on target and also highly repeatable.
Instruments accept a finite corporeality of accuracy and it is important to report measurements within that level of accurateness. S ignificant figures , report the number of digits that are known to some degree of confidence with the measuring device. With increased sensitivity of the equipment , the number of significant figures increases.
Hither is an example which uses the above ideas:
Sue and Jane desire to know the length of the hallway in front end of their classroom. Sue used a slice of yarn that was i meter long. She took the measurement very carefully 3 times and came upwards with the numbers: 11.2 meters, 11.4 meters, and 11.3 meters. Sue took the average and concluded that the hallway is xi.three meters long. Jane used a stick 1 meter long and took the measurement very advisedly 3 times. She came up with the numbers: 12.4 meters, 12.6 meters, and 12.0 meters. Jane ended that the hallway is 12.three meters long. They learned from the builder later that the length of the hallway is 12.4 meters.
-
- 11.2 meters, 11.4 meters, 11.3 meters is Sue's raw data.
-
- 12.4 meters, 12.vi meters, 12.0 meters is Jane's raw data.
-
- Both Sue and Jane are enlightened of the limit of detectability using their instruments. They did not endeavour to measure down to millimeters.
-
- The significant figures of their instruments are both 1 meter. They added an actress digit past estimation.
-
- Sue'south measurement is more than precise than Jane's.
-
- Sue'southward measurement tin not be reproduced by Jane.
-
- According to the data from the builder, Jane's measurements are more authentic than Sue'southward, although they are less precise.
- In trying to figure out why her measurements are not as accurate equally Jane's, Sue realized that she stretched the piece of yarn while measuring the hallway, thus introducing an antiquity into her measurement, leading to an incorrect conclusion.
Lab Activity:
Length
Metric units of length measurement virtually normally used in biology include the meter (m), centimeter (cm), millimeter (mm), micrometer (μm), and nanometer (nm)
How many cm are in a meter? _________
How many μm are in a millimeter? __________
How many mm are in a centimeter? _________ How many nm are in a micrometer? _________
Measuring with Metric
- Obtain a ruler. Find the metric ( centimeters and millimeters) and English units (inches).
How many millimeters are in two centimeters? 2 cm = ______ mm
How many centimeters in 1 inch? one in = _______cm
Use a meter stick or a metric ruler to measure the following:
Width of classroom door opening (in meters) _______ thousand
Length of blackboard (in meters) _______ k
Length of a dollar bill (in centimeters) _______ cm
Width of your pen (in millimeters) _______ mm
Width of a penny (in millimeters) _______ mm
Why is it preferable to measure a penny in millimeters rather than centimeters or meters?
The units micrometer (μm) and nanometer (nm) are useful in microscopy for measuring very tiny objects like cells or even viruses
THE SCIENTIFIC METHOD
The hypothetico-deductive approach underlies most sciences. The procedure has iv stages:
(1) Observations. Events can exist observed either every bit they occur naturally or as the result of experiments. In many cases, instruments such as microscopes or spectrophotometers are used.
(2) Forming hypotheses. A hypothesis is a theory designed to explicate the observations. Assumptions are made in developing the hypothesis.
(3) Predictions can be made based on the hypothesis.
(4) Testing the predictions. Experiments are designed and performed to examination the predictions. The experiments atomic number 82 to new observations, beginning the cycle once again, oftentimes leading to a modified hyptothesis.
Graphing exercises
Fetal Alcohol Syndrome is a serious nativity defect that results from heavy drinking during pregnancy.
You are doing a written report of I.Q. levels of iv thursday graders. Yous are testing 2 groups: Group A – children of mothers who drank less than iv oz. of vino a day during pregnancy; Group B – children of mothers who drank up to a quart of wine a solar day (or its equivalent: a half dozen pack of beer or 6 oz. of scotch.)
| Group A Children (I.Q.) | Group B Children (I.Q.) | |||||||
| 98 | 97 | 105 | 123 | 98 | 101 | 95 | 97 | |
| 102 | 100 | 118 | 107 | 86 | 99 | 96 | 105 | |
| 112 | 91 | 100 | 97 | 103 | 108 | 113 | 86 | |
| 86 | 96 | 115 | 105 | 106 | 92 | 95 | 107 | |
| 116 | 104 | 104 | 111 | 94 | 108 | 105 | 96 | |
Analyze the information by plotting histograms of both groups. Calculate the mean, median and mode I.Q. for both groups. What is your decision?
Lab Exercises
-
- https://openlab.citytech.cuny.edu/bio-oer/biological science-basics/units-of-measure/
-
- https://openlab.citytech.cuny.edu/bio-oer/biology-nuts/quantitative-skills/
-
- http://s3.amazonaws.com/scschoolfiles/747/metric_measurement_lab_activity_for_pre_ap.pdf
-
- https://www.biologyjunction.com/metric_measurement_lab.htm
Source: https://bioclimate.commons.gc.cuny.edu/biology-basics/units-of-measure/
0 Response to "what units would you use to measure a virus"
Postar um comentário